プロフィール・研究紹介Profile / Activities
プロフィール
現在
所属: 九州大学 マス・フォア・インダストリ研究所 先進暗号数理デザイン室
職位: 准教授
学歴
| 2002年3月 | 京都大学理学部 卒業 |
|---|---|
| 2004年3月 | 東京大学大学院数理科学研究科 修士課程 修了 (修士論文題目: On the canonical bundle formula for abelian fiber spaces in positive characteristic) |
| 2007年3月 | 東京大学大学院数理科学研究科 博士課程 修了 (博士論文題目: Torsion points of elliptic curves with good reduction) |
職歴
| 2007年3月~2007年9月 | 東京大学大学院数理科学研究科 研究生 |
|---|---|
| 2007年9月~2015年3月 | 株式会社富士通研究所 研究員 |
| 2015年4月~ | 九州大学 マス・フォア・インダストリ研究所 准教授 |
研究紹介
現在インターネットの普及に伴い、ネットショッピング・インターネット銀行や公的手続きのオンライン申請など、ネットワークを利用した便利なサービスが身近になっている。その一方、秘密情報が漏れないよう情報セキュリティを確保することが課題となっており、情報セキュリティを支えるRSA暗号や楕円曲線暗号などの広く普及している公開鍵暗号の安全性を定期的に評価することは重要な研究テーマである。また近年、クラウドやビッグデータ分析などの進展に伴い、機密データ利活用とプライバシー保護を両立するプライバシー保護データ利活用技術の研究開発が盛んに行われている。そこで、本研究室では以下の2テーマを主に研究している:
(1) 楕円曲線暗号の安全性を支える数学問題の解読計算量評価
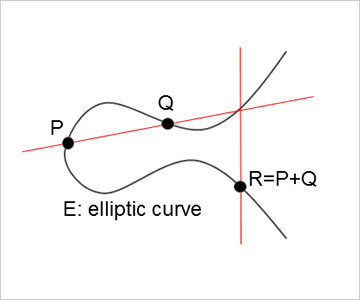
楕円曲線暗号は、1985年にKoblitzとMillerの両氏が独立に考案した暗号で、楕円曲線と呼ばれる数式によって定義された特殊な曲線上の加算法則に基づき暗号化・復号を行う暗号方式である。現在最も利用されている公開鍵暗号のRSA暗号と比べ、楕円曲線暗号はより短い鍵長で同程度の安全性を満たすため、高速処理・省電力を実現できる。楕円曲線暗号の安全性は楕円曲線離散対数問題と呼ばれる数学問題の計算量困難性に依存しており、一部の曲線を除き効率の良い攻撃法は未だ見つかっていない。本研究室では既存の攻撃法の計算量解析の他に、楕円曲線が持つ豊富な数学的性質を利用した効率的な解読法の開発にもチャンレンジしている。
(2) 格子暗号の解読計算量評価と格子ベース準同型暗号の構成・応用
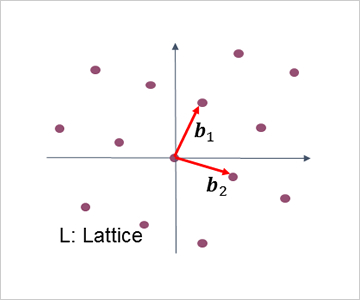
近年、格子暗号は次世代暗号技術として非常に注目されている。格子暗号の安全性は最短ベクトル探索問題などの格子問題の計算量困難性に基づいている。本研究室では、格子問題を効率的に解くための格子基底縮約の開発を行うと共に、格子問題の解読計算量評価を行っている。格子暗号を応用することで、暗号化したまま(復号せずに)加算や乗算ができる準同型暗号を構成することができる。暗号演算の種類により、準同型暗号は3つに分類することができる。具体的には、暗号化したまま加算のみ可能な「加算準同型暗号」、限定回の暗号加算・乗算が可能な「somewhat準同型暗号」、任意の暗号演算が可能な「完全準同型暗号」に大別できる。特に、完全準同型暗号は任意の暗号演算により幅広い応用先が期待される一方、非効率な処理性能のため実用化にはブレークスルーが必要である。本研究室では、処理性能と機能性の両方を併せ持つsomewhat準同型暗号のプライバシー保護データ利活用分野への応用を目指すと共に、効率的な完全準同型暗号の構成にも取り組んでいる。
