Profile / Activities
Profile
At Present
Institute of Mathematics for Industry, Kyushu University
Associate Professor
Education
| 2002 | Bachelor of Science in Mathematics, Kyoto University |
|---|---|
| 2004 | Master of Science in Mathematical Sciences, University of Tokyo Advisor: Professor Toshiyuki Katsura Thesis: On the canonical bundle formula for abelian fiber spaces in positive characteristic |
| 2007 | Ph.D. in Mathematical Sciences, University of Tokyo Advisor: Professor Toshiyuki Katsura Dissertation: Torsion points of elliptic curves with good reduction |
Working Experience
| Apr/2007—Sep/2007 | Mathematical Sciences, University of Tokyo, Research Student |
|---|---|
| Sep/2007 —Mar/2015 | FUJITSU LABORATORIES LTD., Researcher |
| Apr/2015—at present | Institute of Mathematics for Industry, Kyushu University, Associate Professor |
Activities
With widespread of the Internet, convenient services over network, such as shopping, banks, and public procedures over the Internet, are now becoming a familiar presence. On the other hand, it has become an issue to ensure information security in order not to leak confidential information, and hence it is an important research topic to periodically evaluate the security of currently available cryptography such as the RSA cryptosystem and elliptic curve cryptography. In addition, with development of cloud computing and big data analysis, research and development of technology for utilization of confidential data with preserving the privacy has been actively researched. Main research fields of our laboratory are as follows:
(1) Security evaluation of elliptic curve cryptography
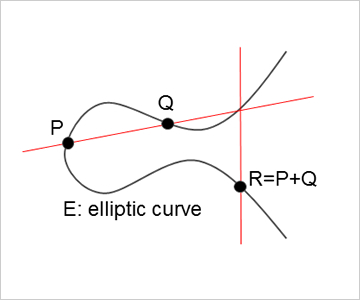
Elliptic curve cryptography was proposed independently by Koblitz and Miller in 1985, which is a cryptosystem using the special addition formula over elliptic curves for both encryption and decryption. Compared to the most available RSA cryptosystem, elliptic curve cryptography ensures that smaller key sizes provide the same security level as RSA, and hence it is useful to be applied in devices with limited processing capacity, storage or power supply, like smart cards. The security of elliptic curve cryptography is based on the computational hardness of the elliptic curve discrete logarithm problem, and efficient attacks for the problem have not yet discovered except for special curves. In our laboratory, we evaluate the complexity of currently known attacks for the problem and also propose new attacks by using mathematical properties of elliptic curves.
(2) Security evaluation of lattice-based cryptography and applications of lattice-based homomorphic encryption
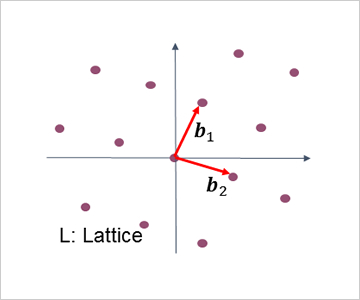
In recent, lattice-based cryptography has been paid attention as a next-generation cryptography. The security of lattice-based cryptography is based on the computational hardness of lattice problems such as the shortest vector problem. In our laboratory, we evaluate the complexity to solve such lattice problems by developing efficient algorithms of lattice basis reduction. We also focus on lattice-based homomorphic encryption, which supports operations on encrypted data (without decryption). Depending on possible operations, homomorphic encryption schemes are classified into the following three types; “additive schemes” supporting only additions, “somewhat homomorphic encryption schemes” supporting a limited number of both additions and multiplications, and finally “fully homomorphic encryption schemes” supporting any operations. In particular, fully homomorphic encryption can be applied to various scenarios, but it needs a breakthrough for practical applications since performance of current schemes is very slow. In our laboratory, we challenge to construct efficient fully homomorphic encryption, and also apply somewhat homomorphic encryption to real applications.
